4 개의 변수로 이루어진 다변량 자료의 상관계수의 행렬이 다음과 같다. 위 상관계수 행렬의 고유값 (eigenvalue) 이 …
문제풀이 모드
0
정답률 : -
4 개의 변수로 이루어진 다변량 자료의 상관계수의 행렬이 다음과 같다. 위 상관계수 행렬의 고유값 (eigenvalue) 이 2.00, 1.79, 0.19, 0.02 일 때, 자료의 총 분산(각 변수의 분산의 합) 중 첫 번째 인자에 의하여 설명될 수 있는 비율은?
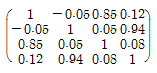
20%
40%
50%
70%
채점하기










